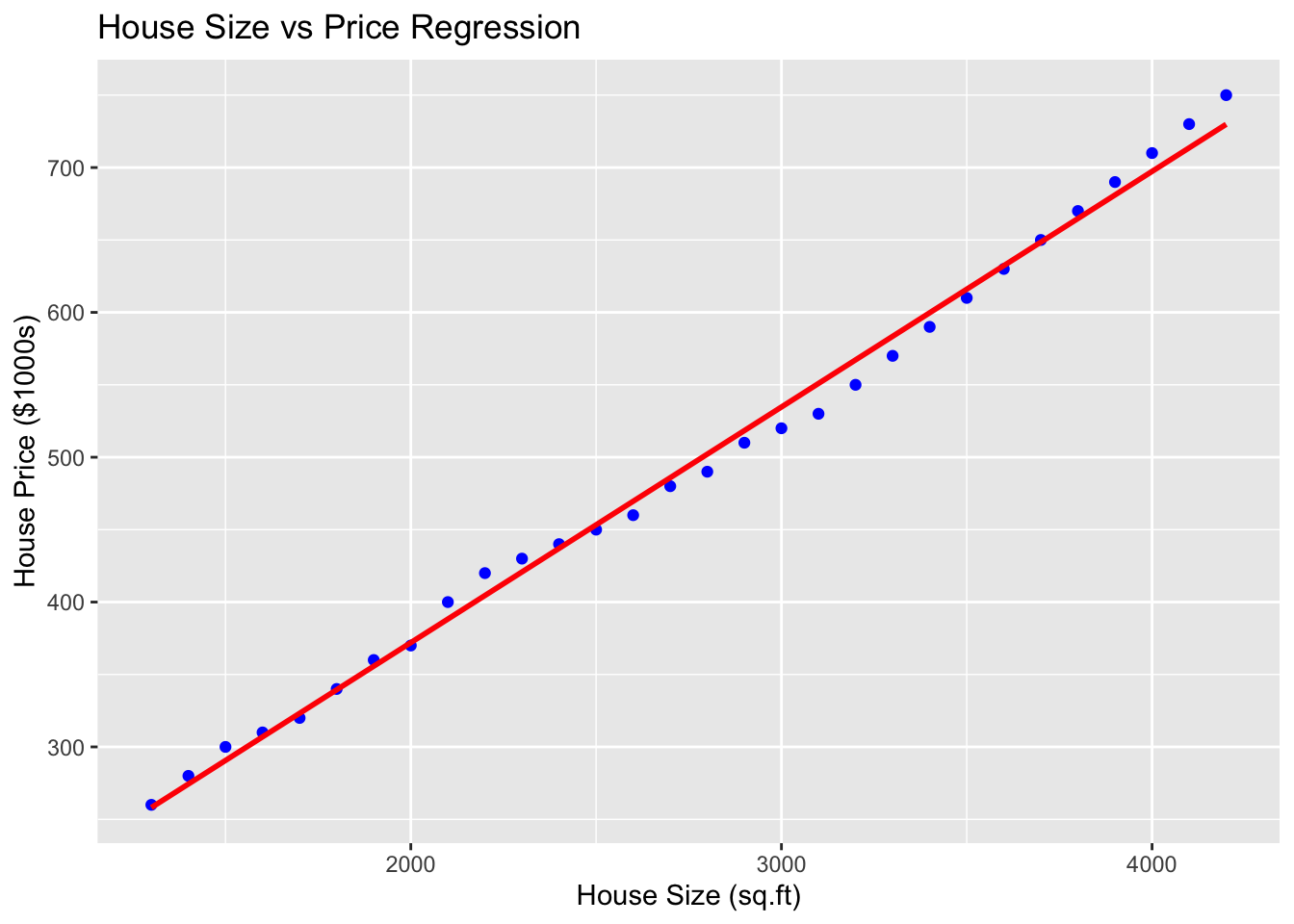
Code
# Load necessary library
library(ggplot2)
# Sample dataset
house_data <- data.frame(
Size = c(1500, 1800, 2100, 2500, 1300, 1700, 2200, 2700, 1600, 1400,
1900, 2300, 2800, 2900, 2000, 2400, 3000, 2600, 3100, 3200,
3300, 3400, 3500, 3600, 3700, 3800, 3900, 4000, 4100, 4200),
Price = c(300, 340, 400, 450, 260, 320, 420, 480, 310, 280,
360, 430, 490, 510, 370, 440, 520, 460, 530, 550,
570, 590, 610, 630, 650, 670, 690, 710, 730, 750)
)
# Fit linear regression model
model <- lm(Price ~ Size, data = house_data)
# Summary of the model
summary(model)
Call:
lm(formula = Price ~ Size, data = house_data)
Residuals:
Min 1Q Median 3Q Max
-20.934 -7.801 1.000 8.098 20.129
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 46.658509 6.500969 7.177 8.23e-08 ***
Size 0.162670 0.002255 72.139 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 10.69 on 28 degrees of freedom
Multiple R-squared: 0.9946, Adjusted R-squared: 0.9945
F-statistic: 5204 on 1 and 28 DF, p-value: < 2.2e-16Code
# Plot the data and regression line
ggplot(house_data, aes(x = Size, y = Price)) +
geom_point(color = "blue") +
geom_smooth(method = "lm", color = "red", se = FALSE) +
labs(title = "House Size vs Price Regression",
x = "House Size (sq.ft)",
y = "House Price ($1000s)")