7  Descriptive Analytics

Descriptive analytics is the foundation of data analysis, focusing on summarizing historical data to extract meaningful insights. It helps organizations understand past trends, identify patterns, and support decision-making through statistical and visual techniques. Unlike predictive or prescriptive analytics, which focus on future trends and recommendations, descriptive analytics primarily deals with “what happened” based on past data.

7.1 Overview of Descriptive Analytics

Descriptive analytics involves processing raw data and presenting it in a meaningful way through summary statistics, visualizations, and structured reports. It is commonly used in business intelligence and research for performance tracking and trend analysis.

7.1.1 Key Characteristics

  • Summarizes past data to provide insights into historical performance.
  • Uses statistical measures to describe the data’s characteristics.
  • Employs data visualization to represent trends and patterns effectively.
  • Forms the basis for advanced analytics like predictive and prescriptive analytics.

7.1.2 Examples of Descriptive Analytics in Action

  • Business: Analyzing monthly sales performance across regions.
  • Healthcare: Monitoring patient admission trends over time.
  • Finance: Tracking daily stock price movements.
  • Marketing: Understanding customer engagement rates on social media.

7.2 Measures of Central Tendency

Measures of central tendency are statistical metrics that summarize or describe the center point or typical value of a dataset. These measures are crucial in data analysis as they provide a simple summary about the sample and the measures. The three main measures of central tendency are the mean, median, and mode. Each measure provides different insights into the distribution and central point of a dataset.

Central tendency measures identify the central point around which data points cluster, offering insights into the dataset’s overall behavior.

  • Mean: The arithmetic average, calculated by summing all observations and dividing by the count of observations.
  • Median: The middle value in an ordered dataset, dividing it into two equal halves.
  • Mode: The most frequently occurring value(s) in a dataset, indicating the highest peak of the distribution.

7.2.1 Mean

The mean, often referred to as the average, is calculated by adding all the numbers in a dataset and then dividing by the count of those numbers. It is the most common measure of central tendency.

  • Formula: \(\text{Mean} = \frac{\sum_{i=1}^{n} x_i}{n}\), where \(x_i\) represents each value in the dataset and \(n\) is the number of values.
  • Sensitive to Outliers: The mean is influenced by outliers (extremely high or low values), which can skew the result.
  • Used for: Interval and ratio levels of measurement.

Example

Consider the set of exam scores: 85, 90, 78, 92, 85.

To calculate the mean:

  1. Sum all the scores: \(85 + 90 + 78 + 92 + 85 = 430\).
  2. Divide by the number of scores: \(430 / 5 = 86\).

So, the mean score is 86.

#### calculation in R:
1.  Create a vector exam_scores containing the given values: 85, 90, 78, 92, 85.
2.  Use the mean() function to compute the average of these values.
3.  Print the result, which will display the mean score.
Code
# Define the vector of exam scores
exam_scores <- c(85, 90, 78, 92, 85)

# Calculate the mean (average) score
mean_score <- mean(exam_scores)

# Print the result
print(mean_score)
[1] 86

Application

The mean is often used in educational settings to calculate the average score of a test, student grades, or even teacher evaluations. It provides a quick snapshot of the overall performance but can be misleading if a few students scored exceptionally high or low compared to the rest.

7.2.2 Median

The median is the middle value in a dataset when the values are arranged in ascending or descending order. If there is an even number of observations, the median is the average of the two middle numbers.

  • Represents: The 50th percentile of the dataset.
  • Not Sensitive to Outliers: Unlike the mean, the median is not affected by outliers, making it a better measure of central tendency for skewed distributions.
  • Used for: Ordinal, interval, and ratio levels of measurement.

Example

Using the same set of exam scores: 85, 90, 78, 92, 85. First, arrange them in ascending order: 78, 85, 85, 90, 92.

The median is the middle number, so in this case, it’s the third score: 85.

If the dataset had an even number of observations, say we add another score, 88, making the set: 78, 85, 85, 88, 90, 92. The median would be the average of the two middle scores, \(85 + 88 = 173\), then \(173 / 2 = 86.5\).

calculation in R:

Code
# Define the vector of exam scores
exam_scores <- c(85, 90, 78, 92, 85)

# Calculate the median score
median_score <- median(exam_scores)

# Print the result
print(median_score)
[1] 85

Application

The median is valuable in real estate to determine the median house price in a region, providing a more accurate representation than the mean, which could be skewed by a few very high-priced or very low-priced sales.

7.2.3 Mode

The mode is the value that appears most frequently in a dataset. A dataset may have one mode (unimodal), more than one mode (bimodal or multimodal), or no mode at all if all values are unique.

  • Useful for: Identifying the most common or popular item in a dataset.
  • Can Be Applied to: Nominal, ordinal, interval, and ratio levels of measurement. It is the only measure of central tendency that can be used with nominal data.
  • Limitations: The mode might not be representative of the dataset as a whole, especially in datasets with a large number of unique values or multiple modes.

Example 1 (unimodal)

In the scores 85, 90, 78, 92, 85, the mode is 85, as it appears more frequently than any other score.

Example 2 (bimodal)

In a different set of scores: 70, 75, 80, 75, 80, 85. The dataset is bimodal because two numbers appear most frequently, 75 and 80.

Example 3 (no mode)

If all scores are unique, for example, 70, 75, 80, 85, 90, there is no mode, as no number appears more than once.

calculation in R:

Code
# Define the vector of exam scores
exam_scores <- c(85, 90, 78, 92, 85)

# Compute mode using which.max()
mode_score <- as.numeric(names(which.max(table(exam_scores))))

# Print the result
print(mode_score)
[1] 85
1.  table(exam_scores): Creates a frequency table of the scores.
2.  which.max(...): Finds the value with the highest frequency.
3.  names(...): Extracts the most frequent score.
4.  as.numeric(...): Converts the result from character to numeric.

Application

The mode is used in marketing research to identify the most popular product size or color. It’s also used in demography to determine the most common age of a population.

When to Use Each Measure

  • Mean: Ideal for datasets without outliers and when every value is relevant. For example, calculating the average temperature of a city over a month to gauge climate change.

  • Median: Best for skewed distributions or when outliers are present, like in income surveys where a few extremely high or low incomes can skew the mean.

  • Mode: Useful for categorical data or to find the most common value in a dataset. For instance, finding the most common shoe size sold in a store to manage inventory efficiently.

Choosing the Right Measure

  • Symmetrical Distributions: The mean is typically preferred for symmetric distributions without outliers, as it considers every value in the dataset.
  • Skewed Distributions: The median is better for skewed distributions or when there are outliers, as it is not influenced by extreme values.
  • Categorical Data: The mode is best for categorical data or when identifying the most common value is of interest.

Importance

Each measure of central tendency offers unique insights into the data. The mean provides a mathematical average, the median gives the midpoint unaffected by outliers, and the mode indicates the most frequently occurring value. Selecting the appropriate measure depends on the nature of the data, its distribution, and the information you seek to extract from it. Understanding these measures enhances our ability to summarize, analyze, and make decisions based on data.

7.3 Measures of Dispersion

Measures of dispersion are statistical tools used to describe the spread or variability within a data set. Unlike measures of central tendency (mean, median, mode) that summarize data with a single value representing the center of the data, measures of dispersion give insights into how much the data varies or how “spread out” the data points are. Understanding the variability helps in comprehending the reliability and precision of the central measures. The primary measures of dispersion include the Range, Interquartile Range (IQR), Variance, Standard Deviation, and Absolute Deviation.

7.3.1 1. Range

The range is the simplest measure of dispersion and is calculated as the difference between the maximum and minimum values in the data set.

Example: For the data set {1, 2, 4, 7, 9}, the range is \(9 - 1 = 8\).

7.3.2 2. Interquartile Range (IQR)

The IQR measures the middle spread of the data, essentially covering the central 50% of data points. It is the difference between the 75th percentile (Q3) and the 25th percentile (Q1).

Example: For the data set {1, 2, 4, 7, 9}, where Q1 is 2 and Q3 is 7, the IQR is \(7 - 2 = 5\).

7.3.3 3. Variance

Variance measures the average of the squared differences from the Mean. It gives a sense of how much the data points deviate from the mean. The formula for variance differs slightly between samples and populations.

  • Population Variance (\(\sigma^2\)): \(\sigma^2 = \frac{\sum (x_i - \mu)^2}{N}\)
  • Sample Variance (\(s^2\)): \(s^2 = \frac{\sum (x_i - \bar{x})^2}{n - 1}\)

Example: For the data set {1, 2, 4, 7, 9}, with a mean of 4.6, the sample variance is calculated as follows:

\[s^2 = \frac{(1-4.6)^2 + (2-4.6)^2 + (4-4.6)^2 + (7-4.6)^2 + (9-4.6)^2}{5-1} = \frac{46.8}{4} = 11.7\]

7.3.4 4. Standard Deviation

The standard deviation is the square root of the variance and provides a measure of dispersion in the same units as the data. It is one of the most commonly used measures of dispersion because it is easily interpreted.

  • Population Standard Deviation (\(\sigma\)): \(\sigma = \sqrt{\sigma^2}\)
  • Sample Standard Deviation (\(s\)): \(s = \sqrt{s^2}\)

Example: Continuing from the variance example, the sample standard deviation of {1, 2, 4, 7, 9} is \(\sqrt{11.7} \approx 3.42\).

7.3.5 5. Absolute Deviation / Mean Absolute Deviation (MAD)

Absolute deviation measures the average distance between each data point and the mean, ignoring the direction (positive or negative). It is a robust measure of variability.

Example: For the data set {1, 2, 4, 7, 9} with a mean of 4.6, the MAD is calculated as follows:

\[MAD = \frac{|1-4.6| + |2-4.6| + |4-4.6| + |7-4.6| + |9-4.6|}{5} = \frac{13.2}{5} = 2.64\]

calculation in R:

Code
# Define the dataset
data <- c(1, 2, 4, 7, 9)

# Calculate Range
data_range <- max(data) - min(data)

# Calculate Interquartile Range (IQR)
data_iqr <- IQR(data)

# Calculate Variance
data_variance <- var(data)

# Calculate Standard Deviation
data_sd <- sd(data)

# Calculate Mean Deviation (Mean Absolute Deviation)
data_mad <- mean(abs(data - mean(data)))

# Print Results
print(paste("Mean Deviation:", data_mad))
[1] "Mean Deviation: 2.72"
Code
print(paste("Standard Deviation:", data_sd))
[1] "Standard Deviation: 3.36154726279432"
Code
print(paste("Variance:", data_variance))
[1] "Variance: 11.3"
Code
print(paste("Range:", data_range))
[1] "Range: 8"
Code
print(paste("Interquartile Range (IQR):", data_iqr))
[1] "Interquartile Range (IQR): 5"

7.4 Measures of Distribution and Association

These measures help in understanding the shape of data distribution and relationships between variables.

7.4.1 Measures of Distribution

  • Skewness: Measures the asymmetry of data distribution.
    • Right-skewed (positive skew): Most values are concentrated on the left.
    • Left-skewed (negative skew): Most values are concentrated on the right.
  • Kurtosis: Measures the “tailedness” of the distribution.
    • High kurtosis: Data has heavy tails (outliers).
    • Low kurtosis: Data has light tails.

7.4.2 Measures of Skewness and Kurtosis

The shape of a dataset’s distribution is characterized by its skewness and kurtosis, offering insights into the data’s symmetry and peakness.

  • Skewness: Indicates the asymmetry of the distribution, with positive skew showing a tail on the right, and negative skew a tail on the left.
  • Kurtosis: Measures the “tailedness” of the distribution, with high kurtosis indicating more variance due to rare extreme deviations.

Understanding these measures helps in identifying the symmetry and the peakedness of the distribution, respectively, which are crucial for analyzing the data’s behavior and making informed decisions.

Skewness

Skewness measures the degree of asymmetry or deviation from symmetry in the distribution of data. A distribution is symmetrical if it looks the same to the left and right of the center point.

  • Zero Skewness: Indicates a perfectly symmetrical distribution.
  • Positive Skewness: Indicates a distribution with a tail that stretches out more towards the positive side of the scale.
  • Negative Skewness: Indicates a distribution with a tail that stretches out more towards the negative side of the scale.

Formula for Skewness: \[ Skewness = \frac{N \sum (X_i - \overline{X})^3}{(N-1)(N-2)S^3} \]

Where:

  • \(N\) is the number of observations,
  • \(X_i\) is each individual observation,
  • \(\overline{X}\) is the mean of the observations,
  • \(S\) is the standard deviation.

Skewness measures the asymmetry of a distribution: - Skewness > 0 → Positively skewed (Right-skewed) - Skewness = 0 → Symmetric (Normal distribution) - Skewness < 0 → Negatively skewed (Left-skewed)

Example of Skewness: Consider a dataset of exam scores: [55, 60, 65, 65, 70, 75, 80]. The distribution of these scores might show slight skewness (positive or negative) depending on how they deviate from the mean. If the data were more concentrated on the lower end (more high scores), the distribution would be positively skewed.

Calculation in R
Code
# Install the package if not already installed
install.packages("moments")

Normal distribution skewness

Code
# Load the library
library(moments)

# Define the dataset
exam_scores <- c(50, 51, 52, 54, 55, 56, 57, 58, 59, 60, 60, 61, 62, 63, 63, 64, 65, 66, 67, 67, 68, 69, 70, 72, 73, 74, 75, 78)

# Calculate Skewness
exam_skewness <- skewness(exam_scores)

# Print the result
print(exam_skewness)
[1] 0.07516543
Histogram
Code
# Load necessary libraries
library(ggplot2)
library(moments)


# Calculate skewness
exam_skewness <- skewness(exam_scores)

# Create histogram with density curve
ggplot(data.frame(exam_scores), aes(x = exam_scores)) +
  geom_histogram(aes(y = after_stat(density)), bins = 5, fill = "blue", color = "black", alpha = 0.6) +
  geom_density(color = "red", linewidth = 1) +
  labs(title = paste("Histogram and Density Curve of Exam Scores\nSkewness:", round(exam_skewness, 2)),
       x = "Exam Scores",
       y = "Density") +
  theme_minimal()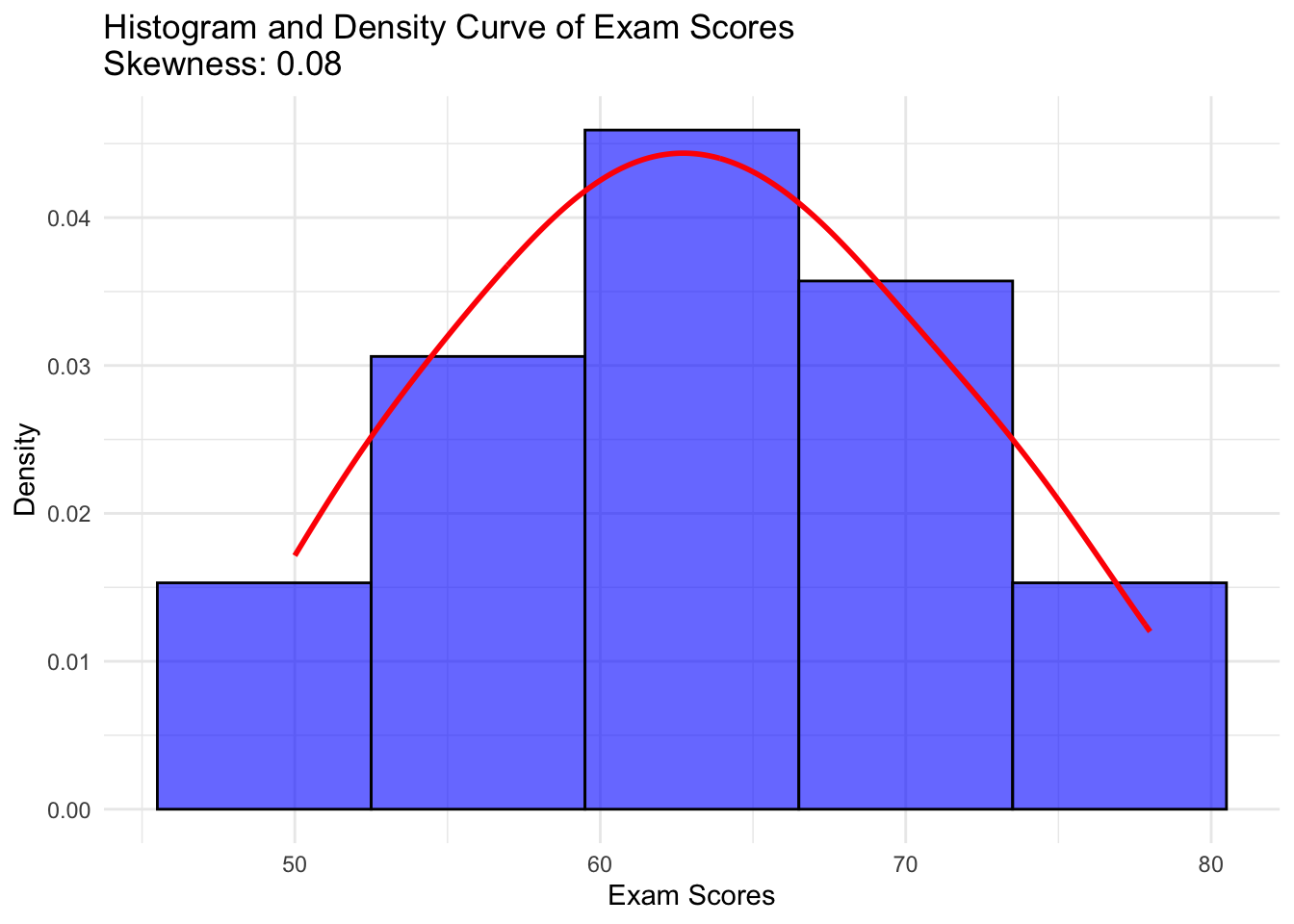

Left skewed

Code
# Load the library
library(moments)

# Define the dataset
exam_scores <- c(50, 53, 55, 55, 56, 57, 58, 58, 59, 59, 60, 60, 61, 61, 61, 62, 62, 62, 63, 63, 63, 64, 64, 64, 65, 65, 66, 66)

# Calculate Skewness
exam_skewness <- skewness(exam_scores)

# Print the result
print(exam_skewness)
[1] -0.7368719
Histogram
Code
# Load necessary libraries
library(ggplot2)
library(moments)


# Calculate skewness
exam_skewness <- skewness(exam_scores)

# Create histogram with density curve
ggplot(data.frame(exam_scores), aes(x = exam_scores)) +
  geom_histogram(aes(y = after_stat(density)), bins = 5, fill = "blue", color = "black", alpha = 0.6) +
  geom_density(color = "red", linewidth = 1) +
  labs(title = paste("Histogram and Density Curve of Exam Scores\nSkewness:", round(exam_skewness, 2)),
       x = "Exam Scores",
       y = "Density") +
  theme_minimal()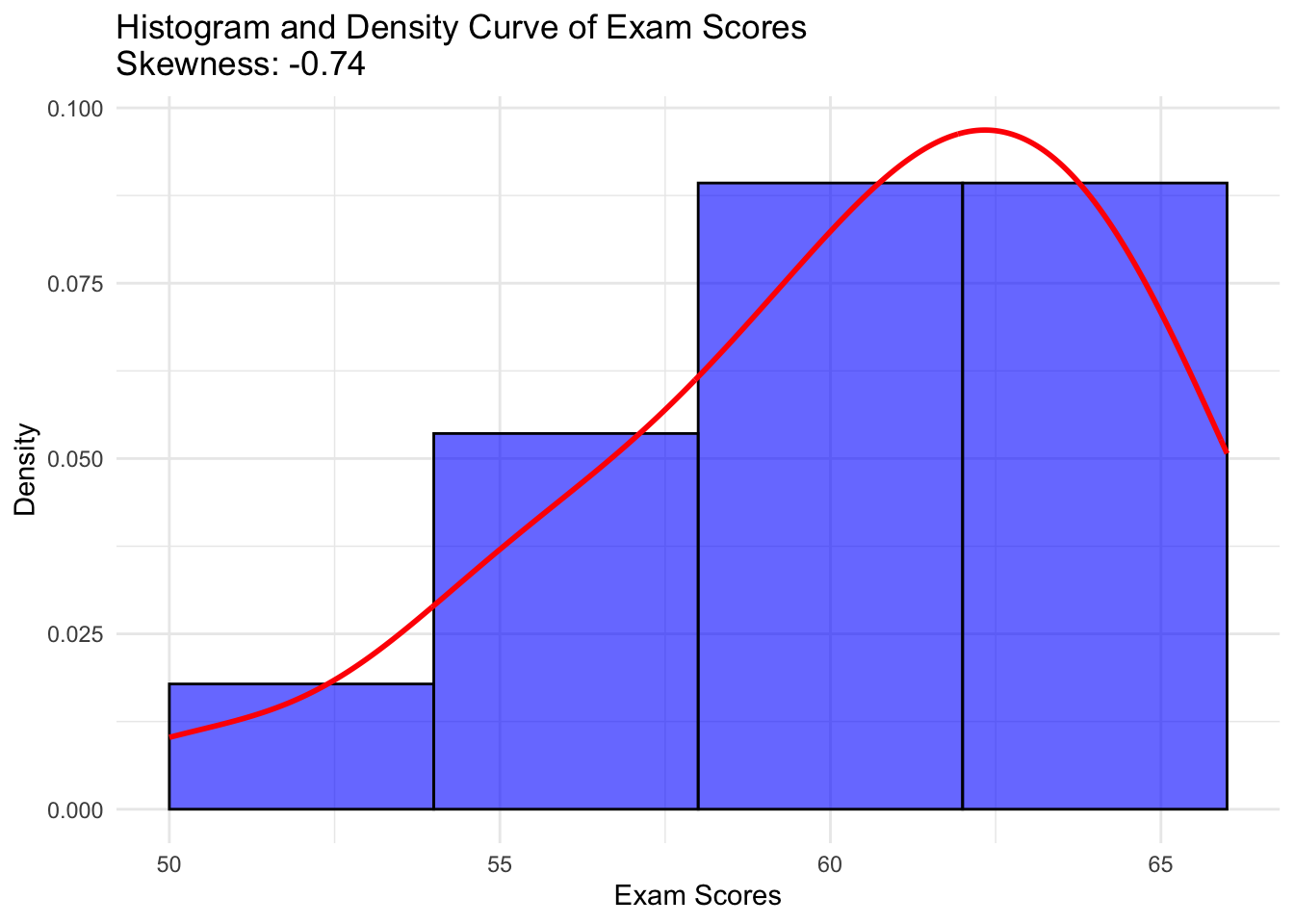

Right skewed

Code
# Load the library
library(moments)

# Define the dataset
exam_scores <- c(5, 7,8, 9, 10, 11, 12, 13, 14, 15, 16,17, 18, 19, 20, 21, 22, 23, 24,25, 26, 27, 28, 30, 32, 35, 38, 40, 42)

# Calculate Skewness
exam_skewness <- skewness(exam_scores)

# Print the result
print(exam_skewness)
[1] 0.4172705
Histogram
Code
# Load necessary libraries
library(ggplot2)
library(moments)


# Calculate skewness
exam_skewness <- skewness(exam_scores)

# Create histogram with density curve
ggplot(data.frame(exam_scores), aes(x = exam_scores)) +
  geom_histogram(aes(y = after_stat(density)), bins = 5, fill = "blue", color = "black", alpha = 0.6) +
  geom_density(color = "red", linewidth = 1) +
  labs(title = paste("Histogram and Density Curve of Exam Scores\nSkewness:", round(exam_skewness, 2)),
       x = "Exam Scores",
       y = "Density") +
  theme_minimal()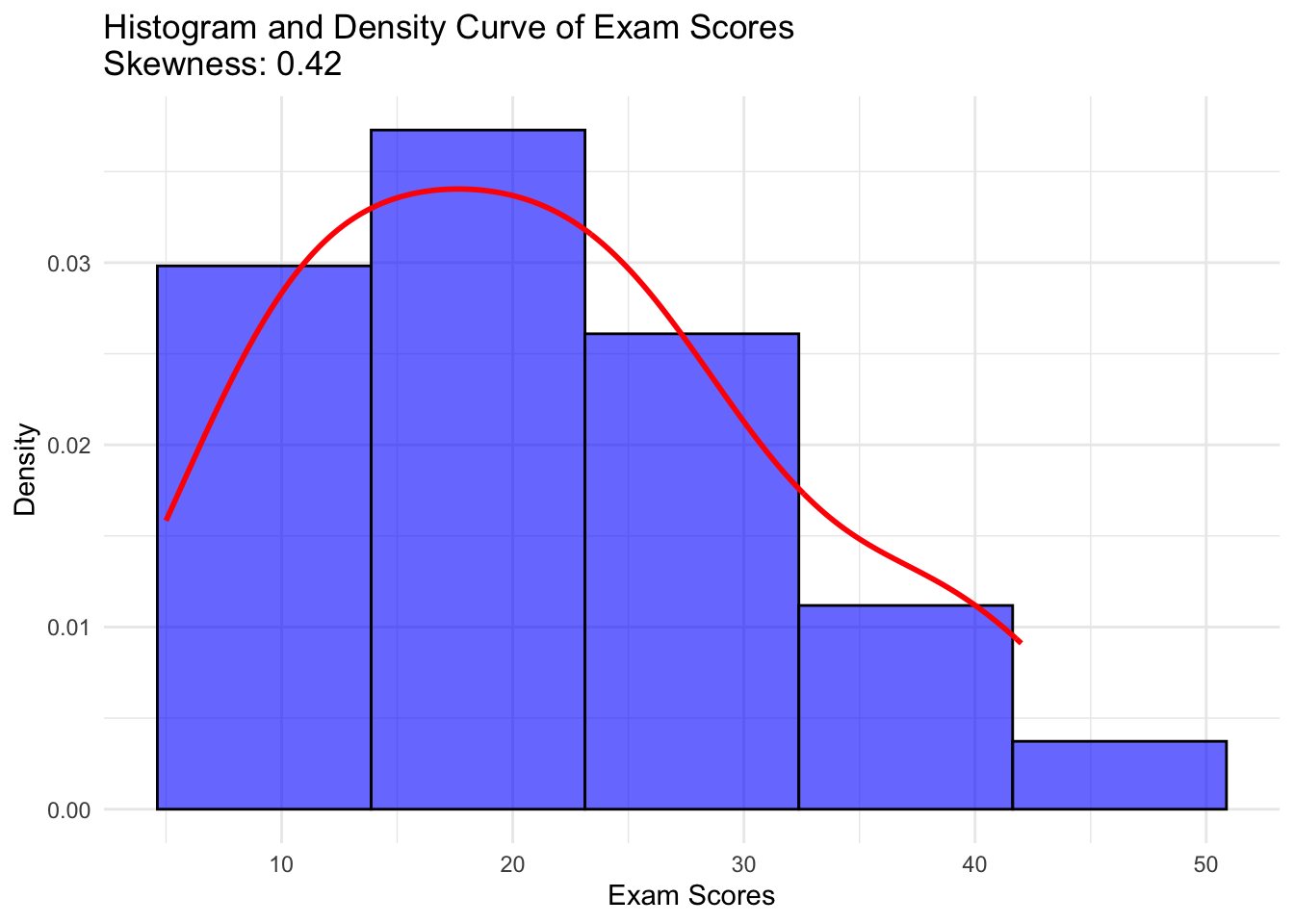

Kurtosis

Kurtosis measures the “tailedness” of the distribution or the peakedness. It indicates how much of the data is concentrated in the tails and the peak of the distribution relative to a normal distribution.

  • Mesokurtic (Kurtosis = 3): Indicates a distribution with kurtosis similar to that of a normal distribution. It is referred to as mesokurtic.
  • Leptokurtic (Kurtosis > 3): Indicates a distribution that is more peaked than a normal distribution, with fatter tails. Such distributions have more extreme values (outliers).
  • Platykurtic (Kurtosis < 3): Indicates a distribution that is flatter than a normal distribution with thinner tails. Such distributions have fewer extreme values.

Formula for Kurtosis: \[ Kurtosis = \frac{N(N+1) \sum (X_i - \overline{X})^4}{(N-1)(N-2)(N-3)S^4} - \frac{3(N-1)^2}{(N-2)(N-3)} \]

Where:

  • The symbols represent the same quantities as in the skewness formula.

Kurtosis measures the “tailedness” of the distribution:

  • Kurtosis > 3 → Leptokurtic (Heavy tails)
  • Kurtosis = 3 → Mesokurtic (Normal distribution)
  • Kurtosis < 3 → Platykurtic (Light tails, flat distribution)

Example of Kurtosis: Consider a dataset representing the heights of a group of people. If most people are of average height, with few very short or very tall people, the distribution might be leptokurtic, indicating a peaked distribution with fat tails.

Calculation in R
Code
# Load the library
library(moments)

# Define the dataset
exam_scores <- c(55, 60, 65, 65, 70, 75, 80)

# Calculate Skewness
exam_kurt <- kurtosis(exam_scores)

# Print the result
print(exam_kurt)
[1] 1.984131
Histogram
Code
# Load necessary libraries
library(ggplot2)
library(moments)

# Define the dataset
exam_scores <- c(55, 60, 65, 65, 70, 75, 80)

# Create a dataframe
exam_data <- data.frame(Score = exam_scores)

# Plot histogram with density curve
ggplot(exam_data, aes(x = Score)) +
  geom_histogram(aes(y = after_stat(density)), bins = 5, fill = "blue", alpha = 0.5, color = "black") +
  geom_density(color = "red", linewidth = 1) +
  labs(title = "Histogram and Density Curve of Exam Scores",
       x = "Exam Scores",
       y = "Density") +
  theme_minimal()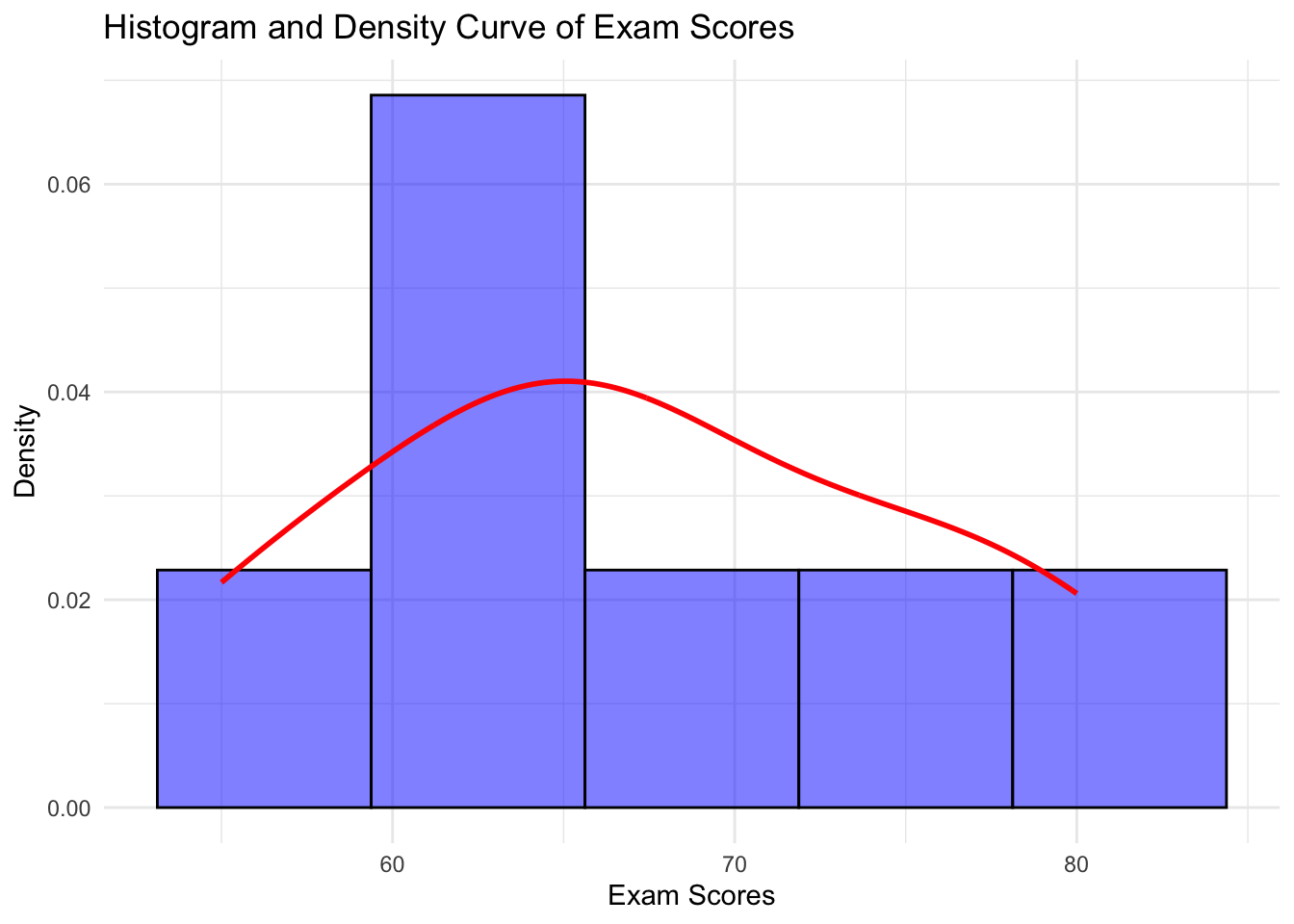

Application
  • Finance: Skewness and kurtosis are used to analyze the distribution of returns for an investment, helping to understand the risk and the likelihood of extreme outcomes.
  • Quality Control: In manufacturing, these measures help in identifying the deviation from the process standards.
  • Environmental Science: Analyzing rainfall or temperature data to understand the distribution and the occurrence of extreme weather conditions.

7.4.3 Measures of Association

These indicate relationships between two variables. - Correlation: Measures the strength and direction of association between two variables. - Pearson’s correlation: Measures linear relationship. - Spearman’s rank correlation: Measures monotonic relationship. - Covariance: Measures the degree to which two variables vary together.

Example in R

Code
cor(mtcars$mpg, mtcars$hp)  # Correlation between MPG and Horsepower
[1] -0.7761684
Code
cov(mtcars$mpg, mtcars$hp)  # Covariance between MPG and Horsepower
[1] -320.7321

Scatter Plot

Code
# Load necessary library
library(ggplot2)

# Scatter plot with regression line
ggplot(mtcars, aes(x = hp, y = mpg)) +
  geom_point(color = "blue", size = 3, alpha = 0.7) +  # Scatter plot points
  geom_smooth(method = "lm", color = "red", se = FALSE) +  # Regression line
  labs(title = "Scatter Plot of MPG vs Horsepower",
       x = "Horsepower (hp)",
       y = "Miles Per Gallon (mpg)") +
  theme_minimal()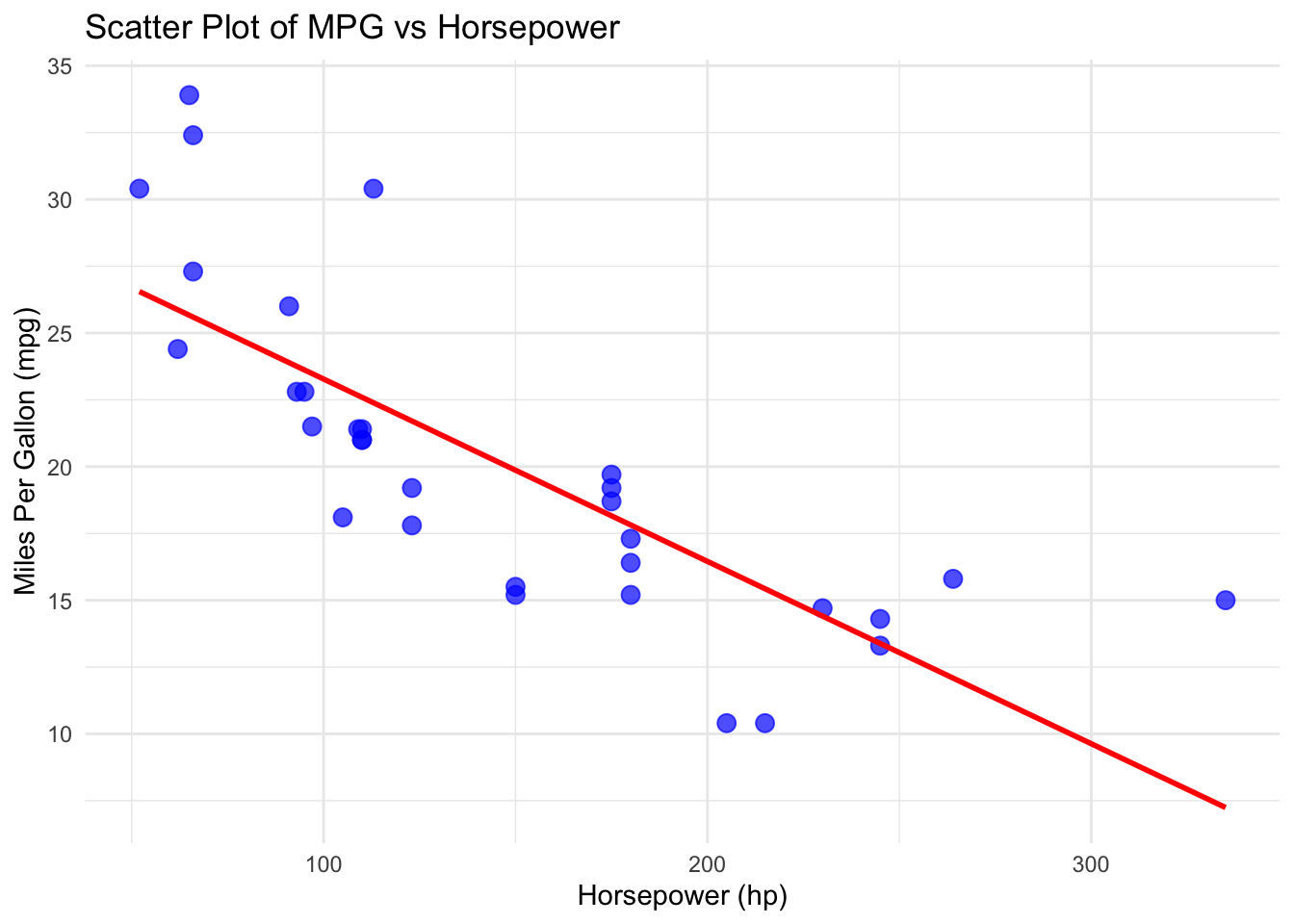

Positive Correlation

Code
# Create a simple data frame
students <- data.frame(
  Name = c("Arun", "Arun", "Charan", "Divya", "Eswar", 
           "Fathima", "Gopal", "Harini", "Ilango", "Jayanthi"),
  Age = c(25, 25, 35, 28, 22, 40, 33, 27, 31, 29),
  Height = c(5.6, 5.6, NA, 5.4, 6.0, 5.3, 5.9, 5.5, 5.7, 5.8),
  Gender = c("M", "M", NA, "F", "M", "F", "M", "F", "M", "F"),
  Marks = c(85, 85, 78, 88, 76, 95, 82, 89, 80, 91),
  Attendance = c(92, 92, 88, 90, 87, 95, 83, 89, 86, 91)  
)
cor(students$Attendance , students$Marks)  # Correlation 
[1] 0.711283
Code
# Load necessary library
library(ggplot2)

# Scatter plot with regression line
ggplot(students, aes(x = Attendance, y = Marks)) +
  geom_point(color = "blue", size = 3, alpha = 0.7) +  # Scatter plot points
  geom_smooth(method = "lm", color = "red", se = FALSE) +  # Regression line
  labs(title = "Scatter Plot",
       x = "Attendance",
       y = "Marks") +
  theme_minimal()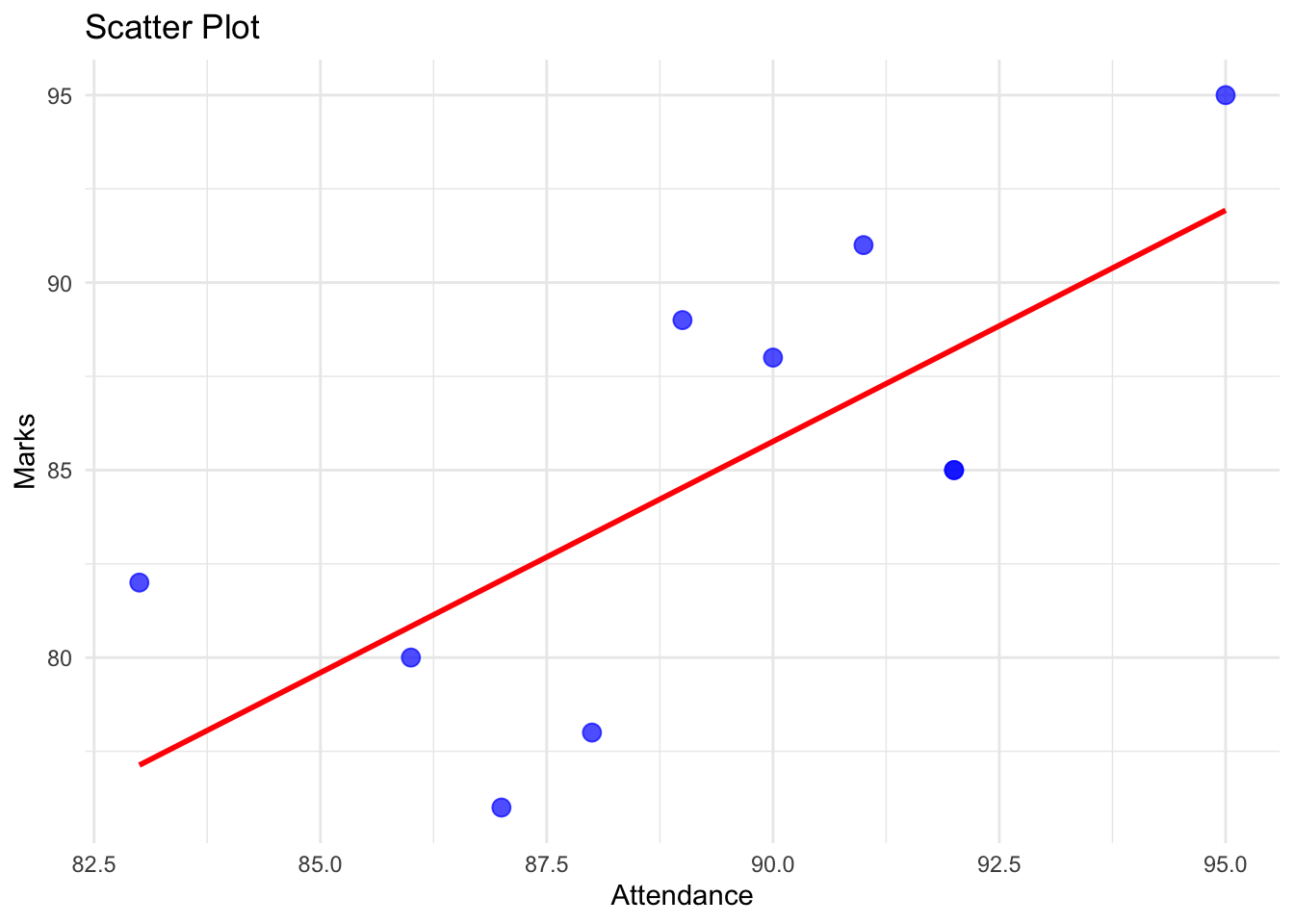

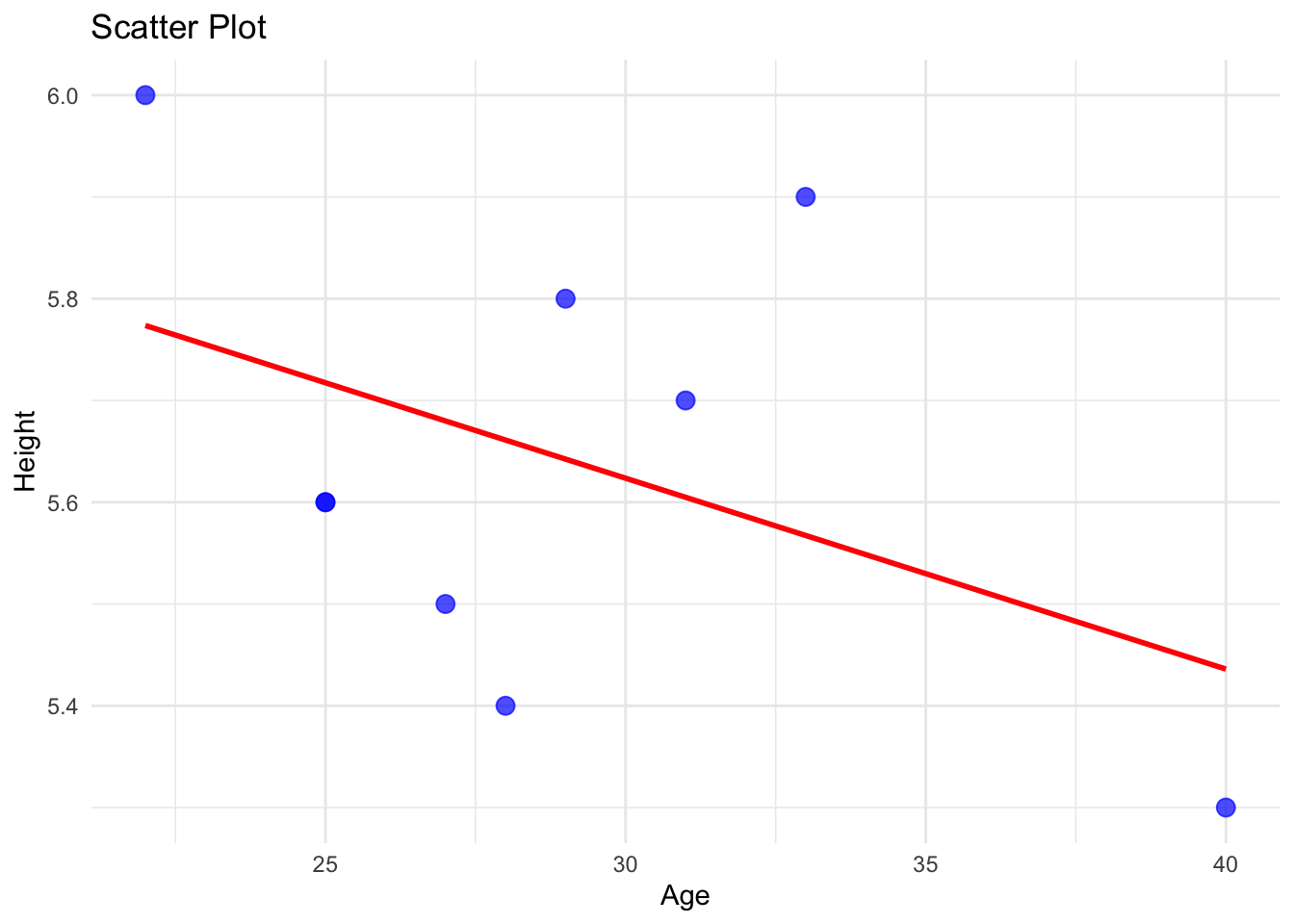
Negative Correlation

Code
cor(students$Age , students$Height)  # Correlation 
[1] NA
Code
# Load necessary library
library(ggplot2)

# Scatter plot with regression line
ggplot(students, aes(x = Age, y = Height)) +
  geom_point(color = "blue", size = 3, alpha = 0.7) +  # Scatter plot points
  geom_smooth(method = "lm", color = "red", se = FALSE) +  # Regression line
  labs(title = "Scatter Plot",
       x = "Age",
       y = "Height") +
  theme_minimal()